Sein oder Nichtsein: Bessere Tests für die Existenz der „Schrödinger-Katze“
Wissenschaftler am MPQ entwickeln neue Beweisverfahren für den makroskopischen Realismus
Zwei fundamentale Annahmen kennzeichnen das Weltbild des lokalen Realismus: Zum einen liegen die Eigenschaften von Objekten nicht im Auge des Betrachters, sondern sind fest vorgegeben. Zum andern können sich physikalische Einflüsse niemals schneller als mit Lichtgeschwindigkeit ausbreiten. 1964 entdeckte John Bell, dass sich aus diesen Annahmen Einschränkungen für die möglichen Korrelationen zwischen Messungen an räumlich getrennten Objekten ergeben. Diese werden heute auch als die „Bell’schen Ungleichungen“ bezeichnet.
1984 bewies Arthur Fine, dass alle lokal-realistischen Theorien den Bell’schen Ungleichungen genügen müssen. Darüber hinaus lässt sich aus der Gültigkeit der Bell’schen Ungleichungen folgern, dass es für die beobachteten Daten eine lokal-realistische Erklärung gibt. In den vergangenen Jahrzehnten haben quantenphysikalische Experimente wiederholt mit immer höherer Genauigkeit belegt, dass die Bell’schen Ungleichungen verletzt werden können, z.B. wenn man es mit verschränkten Quanten-Zuständen von zwei oder mehr Systemen zu tun hat.
Damit wurde das Weltbild des lokalen Realismus in Bezug auf die räumlichen Korrelationen von Objekten schlüssig widerlegt. Auch in der Quantenmechanik gilt jedoch die „no-signalling“-Annahme, dass Signalübertragung mit Überlichtgeschwindigkeit nicht möglich ist. Sie gehört zu den festen Säulen der Speziellen Relativitätstheorie, und ihre Verletzung stände im Widerspruch zur Kausalität: sie würde implizieren, dass man mit der Vergangenheit kommunizieren kann. Quantenexperimente können daher nur die Bell’schen Ungleichungen verletzen, nicht jedoch die „no-signalling“ Annahme.
Das Gegenstück zur Verschränkung von Quantensystemen, aus der sich die Verletzung der Bell‘schen Ungleichungen beim lokalen Realismus ergibt, ist das berühmte Paradoxon der „Schrödinger Katze“ als Test für die Gültigkeit des makroskopischen Realismus. Gemäß diesem „Gedankenexperiment“ kann die Katze in einen Überlagerungszustand gebracht werden, in dem sie gleichzeitig tot und lebendig ist. Solche Überlagerungszustände existieren erwiesenermaßen für mikroskopische Objekte. Die meisten Physiker hadern jedoch mit dem Umstand, dass die Quantenmechanik im Prinzip ein solches seltsames Verhalten auch auf makroskopischer Skala erlauben würde. Im Weltbild des makroskopischen Realismus ist eine Superposition makroskopischer Zustände dagegen strikt verboten, und makroskopische Objekte können gemessen werden, ohne sie gleichzeitig zu verändern.
1985 zeigten Anthony Leggett und Anupam Garg, dass sich aus den Annahmen des makroskopischen Realismus Einschränkungen ergeben in Bezug auf die zeitlichen Korrelationen, die zwischen aufeinander folgenden Messungen an einem einzelnen Quantensystem auftreten können. Analog zu den Bell’schen Ungleichungen für den lokalen Realismus lassen sich somit auch für den makroskopischen Realismus Ungleichungen definieren, denen diese zeitlichen Korrelationen genügen müssen.
In den vergangenen Jahren wurden diese „Leggett-Garg-Ungleichungen“ in vielen Experimenten verletzt, allerdings nur mit mikroskopischen Quantensystemen, die den makroskopischen Realismus nicht widerlegen können. Ob es tatsächlich möglich ist, makroskopische Objekte wie eine ausgewachsene Katze in einen Superpositionszustand zu bringen, ist experimentell noch nicht entschieden. Es ist eine der spannendsten noch offenen Fragen, die die Grundlagen der Physik betreffen.
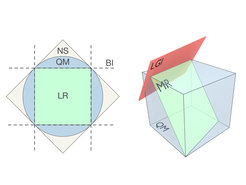
Auch wenn es im lokalen Realismus um räumliche Korrelationen zwischen wenigstens zwei Systemen geht und beim makroskopischen Realismus um zeitliche Korrelationen von Messungen an einem einzelnen Objekt, so bestehen doch viele Analogien zwischen den Konzepten, und die entsprechenden Bell’schen und Leggett-Garg‘schen Ungleichungen sind in ihrer mathematischen Struktur fast identisch. Die Arbeit von Clemente und Kofler hat nun einen bemerkenswerten und bislang unbekannten fundamentalen Unterschied aufgedeckt: mit einer ausgeklügelten Analyse der Dimensionen von Wahrscheinlichkeitsräumen gelang es ihnen zu beweisen, dass das von Arthur Fine für den lokalen Realismus postulierte Theorem nicht auf das Weltbild des makroskopischen Realismus übertragen werden darf. Mit anderen Worten, die Leggett-Garg-Ungleichungen bilden – im Gegensatz zu den Bell’schen Ungleichungen für den lokalen Realismus – keine optimale Grenze für die makro-realistischen Theorien (siehe Abbildung).
Der Grund dafür ist interessanterweise die zeitliche Analogie zu der „no-signalling“-Annahme. Die „no-signalling-in-time“ Annahme fordert, dass die Ergebnisse späterer Messungen an makroskopischen Objekten nicht von früheren Messungen abhängen dürfen. Diese Regel gilt im makroskopischen Realismus, wird aber in der Quantenmechanik verletzt. „Im Gegensatz zu den Leggett-Garg-Ungleichungen ist die Kombination aller „no-signalling-in-time“-Bedingungen sowohl notwendig als auch hinreichend für den makroskopischen Realismus“, erklärt Clemente. „Das offenbart einen entscheidenden Unterschied zwischen den räumlichen Korrelationen bei Tests des lokalen Realismus und den zeitlichen Korrelationen bei Tests des makroskopischen Realismus.“
Physiker, die mit ihren Experimenten den makroskopischen Realismus widerlegen wollen, sollten sich demzufolge nicht mehr auf die Legget-Garg-Ungleichungen fokussieren, wie sie es viele Jahre lang gemacht haben. „Die Leggett-Garg Ungleichungen schränken den Parameterraum, in dem mögliche Verletzungen des makroskopischen Realismus gefunden werden können, unnötig stark ein“, ergänzt Kofler. „Die ‚no-signalling-in-time’-Bedingung ist nicht nur besser, sondern sogar optimal für experimentelle Tests, ob die Schrödinger-Katze in der Natur existieren kann.“ Olivia Meyer-Streng












