Mit Exzitonen Billard spielen
Neuer Werkzeugkasten für die Simulation ultraflacher Halbleiter entwickelt
Halbleiter spielen eine wichtige Rolle, sei es in der Elektronik, Optoelektronik oder Photovoltaik. Doch wie andere Festkörper sind sie Quanten-Vielteilchensysteme. Daher würde eine Berechnung ihrer Materialeigenschaften herkömmliche Computer überfordern. Diese Aufgabe könnte aber ein Quantensystem mit vergleichbaren Eigenschaften übernehmen, das von außen voll kontrollierbar ist. Diesen Traum von einem Quantensimulator gibt es schon lange. Nun ist der von Richard Schmidt geleiteten Theorie-Nachwuchsgruppe am Max-Planck-Institut für Quantenoptik in Zusammenarbeit mit Kollegen an der Universität Hamburg und ETH Zürich eine Arbeit gelungen, die eine erfolgreiche Simulation bestimmter Eigenschaften eines ultraflachen Halbleiters erklären kann. Mehr noch, sie ist ein neuer Werkzeugkasten, um diese zweidimensionalen Halbleiter theoretisch zu beschreiben.
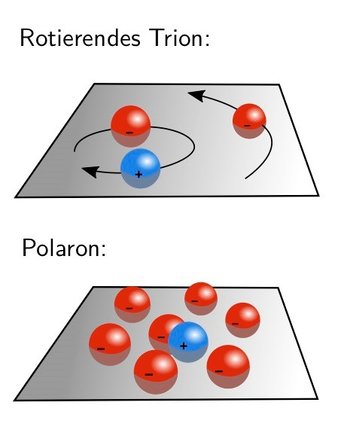
Obere Grafik: Links ist das Exziton, das aus einem Loch (blau, positiv geladen) und einem Elektron (rot, negativ) besteht, zu sehen. Es hat gerade ein weiteres Elektron (rechts) „eingefangen“ und bildet so ein Trion, ein Quasiteilchen, das aus drei Teilchen besteht.
Untere Grafik: Im zweidimensionalen Halbleiter sammeln sich frei bewegliche Elektronen um ein Exziton (Mitte) und bilden mit ihm zusammen ein größeres Quasiteilchen, ein Polaron.
Nicht nur in der menschlichen Gesellschaft allgemein, auch in der Physik gibt es unterschiedliche „Kulturen“. Die jüngste Arbeit aus der von Richard Schmidt geleiteten Theorie-Nachwuchsgruppe am Max-Planck-Institut für Quantenoptik schlägt einen verbindenden Bogen zwischen zwei solchen Physikkulturen: Quantenoptik und Festkörperphysik. Und sie ist Teil einer Forschungsrichtung, die eine Art analogen Quantencomputer, sogenannte Quantensimulatoren, entwickelt. Diese Idee geht auf den berühmten amerikanischen Theoretiker Richard Feynman zurück.
Publiziert wurde die Arbeit der Garchinger Theoretiker nun als Empfehlung der Herausgeber (Editor’s suggestion) in „Physical Review B“. In ihr geht es um ein Festkörpersystem mit besonderen Eigenschaften, die einige Jahre zuvor zum ersten Mal in ultrakalten Quantengasen beobachtet wurden. Solche Gase sind ein beliebtes Untersuchungsobjekt der Quantenoptik und haben als Quantensimulator eine Vorhersage für ein spezielles System der Festkörperphysik ermöglicht, die kürzlich experimentell nachgewiesen wurde.
Um den Hintergrund zu verstehen, muss man zuerst die Idee der Quantensimulation in diesem Kontext verstehen. Festkörper bestehen aus extrem vielen Teilchen. In ihnen sind die Atome mit ihren Elektronen auf engstem Raum zu einem Kristallgitter „gestapelt“ und bilden damit ein komplexes Quanten-Vielteilchensystem. Solche Systeme sind das Spezialgebiet von Richard Schmidt, dem Leiter der Forschergruppe. Dieses Vielteilchensystem kann im Kollektiv komplexe Eigenschaften hervorbringen, auf denen in Halbleitermaterialien die Elektronik und die Optoelektronik von LEDs bis zur Photovoltaik beruhen.
Das grundsätzliche Problem der theoretischen Physik besteht nun darin, dass sie zwar die exakten quantenmechanischen Gleichungen für ein solches Vielteilchensystem wie einen Festkörper formulieren kann – sie kann diese aber nicht exakt lösen. Daher müssen die Theoretiker mit stark vereinfachenden Lösungen arbeiten. Genauere Resultate könnte zwar im Prinzip eine Simulation liefern, also ein virtueller Nachbau des betrachteten Festkörpers im Computer. Das allerdings scheitert an den komplexen Wechselwirkungen der Quantenteilchen untereinander. Schon ein Quantensystem aus sehr wenigen Teilchen lässt die erforderliche Rechenleistung so explodieren, dass auch die besten heutigen Supercomputer überfordert wären.
Feynmans smarte Idee eines Quantensimulators
Dieses Dilemma brachte Richard Feynman bereits in den 1980er-Jahren auf eine smarte Idee: Man könnte ein solches Quanten-Vielteilchensystem durch ein ähnlich mächtiges Quantensystem simulieren. Dieses andere Quantensystem müsste vergleichbare Eigenschaften haben, aber offen zugänglich und damit voll kontrollierbar sein – im Gegensatz zu typischen Festkörpersystemen.
Hier kommen nun die ultrakalten Quantengase der Quantenoptik ins Spiel. Im Prinzip bringen sie genau das mit, was einen Quantensimulator charakterisiert: Sie sind von außen voll kontrollierbar und so mit den Eigenschaften eines Festkörpersystems programmierbar. Um ein ultrakaltes Quantengas zu erzeugen, wird eine Wolke aus im Vakuum schwebenden Atomen auf extrem niedrige Temperaturen abgekühlt, nur wenige Millionstel Grad über dem absoluten Temperaturnullpunkt. Nun kann man zum Beispiel die durch die Kälte in ihrer Bewegung eingefrorenen Atome in den Kreuzungspunkten eines räumlichen Gitters aus Laserstrahlen einfangen. Besitzen diese Atome geeignete Eigenschaften, dann können sie das Verhalten bestimmter Elektronen in einem Festkörperkristall simulieren. Dazu muss man wissen, dass Elektronen die wesentlichen Eigenschaften eines Festkörpers bestimmen, etwa seine Härte, ob er Licht in elektrischen Strom umwandeln kann oder umgekehrt – oder seine elektrische Leitfähigkeit bis hin zur Supraleitung bei bestimmten Materialien.
Das ist die Idee. In der Praxis besteht die Herausforderung für die Quantenoptik aber seit vielen Jahren darin, die Wechselwirkung zwischen den Elektronen in einem Festkörper richtig nachzubilden. Elektronen als elektrische Elementarladungen wechselwirken untereinander noch über relativ große Distanzen, über elektrische und magnetische Felder. Sie beeinflussen also nicht allein ihre nächsten Nachbarn, sondern auch die übernächsten und so weiter. Kalte Atome in einem Quantengas hingegen verhalten sich eher wie Billardkugeln: Sie wechselwirken über Stöße im Wesentlichen nur mit ihren nächsten Nachbarn.
Das Exziton als Billardkugel
Um also einen solchen Quantensimulator auf einen Festkörper anwenden zu können, wäre es hilfreich, wenn es auch im Festkörpersystem Teilchen gäbe, die eher wie Billardkugeln wechselwirken. Tatsächlich gibt es diese in der Form sogenannter Exzitonen. Diese Teilchen kommen in jedem normalen Halbleiter vor, zum Beispiel in einer leuchtenden LED oder umgekehrt in einer Strom produzierenden Photovoltaikanlage.
Ein Exziton entsteht zum Beispiel, wenn ein Lichtquant auf ein Elektron in einem Halbleitermaterial trifft. Passt die Energie des Photons, dann nimmt das Elektron diese Energie auf, löst sich von seinem Atom und kann sich frei durch den Halbleiter bewegen. Das passiert, wenn Licht in Strom umgewandelt wird. Auf dem ursprünglichen Platz des Elektrons entsteht nun ein Loch, das sich effektiv als elektrisch positive Ladung ebenfalls durch das Kristallgitter bewegen kann. Das Elektron und das Loch ziehen sich gegenseitig elektrisch an und bilden gemeinsam ein sogenanntes Quasiteilchen, das Exziton, das sich nun auch frei durch den Halbleiter bewegen kann.
„Man kann es sich ungefähr wie ein Wasserstoffatom vorstellen“, erklärt Richard Schmidt: „Das Loch entspricht dem Proton in dessen Atomkern.“ Und dieses Exziton verhält sich eher wie eine Billardkugel, die nur im direkten Kontakt eine andere Kugel anstoßen kann – wie die Atome im kalten Quantengas. Allerdings sind das Elektron und das Loch des Exzitons in gewöhnlichen Halbleitern ziemlich weit voneinander entfernt. „Das können zehn oder mehr Nanometer sein“, sagt Christian Fey, Postdoktorand in der Garchinger Gruppe und Erstautor der wissenschaftlichen Arbeit. Befinden sich nun in einem normalen, dreidimensionalen Halbleiter weitere frei bewegliche Elektronen, dann umgeben diese das Exziton nicht nur, sie durchdringen und zerlegen es recht schnell. Das geschieht zum Beispiel bei Elektronendichten, die technisch relevant sind.
Ultraflache Halbleiter als ideales Simulationsobjekt
Ein zweidimensionaler Halbleiter hingegen ist so flach, dass sich ober- und unterhalb des Exzitons keine Elektronen aufhalten, die es schwächen können. Das Exziton kann sogar stabil überleben, wenn sich zusätzliche Elektronen in der Ebene befinden. Und nicht nur das: Es kann die Elektronen um sich herum auch so beeinflussen, dass ein sogenanntes Polaron entsteht. Das ist ein Vielteilchenobjekt, in dem das Exziton in eine Wolke aus Elektronen „eingekleidet“ ist. Die Masse des Exzitons wird effektiv erhöht, da es diese Wolke mit durch den Festkörper ziehen muss. Alternativ zur Polaronbildung kann das Exziton auch mit einem weiteren Elektron als drittes Teilchen ein größeres Quasiteilchen bilden, ein „Trion“. „Das ist wie ein Sonnensystem mit einem Stern und einem Planeten, das einen aus dem Kosmos vorbeikommenden Kometen als dritten Körper einfängt“, erklärt Schmidt. „Wir haben sogar theoretisch einen neuen Zustand gefunden, in dem das Elektron gegensinnig um das Exziton kreist“, ergänzt Fey, „das wäre so, als würde der Komet in Gegenrichtung zu dem Planeten um den Stern herumlaufen.“
Dieser Zustand ist experimentell noch nicht nachgewiesen, aber ihn und noch andere physikalische Eigenschaften eines zweidimensionalen Halbleiterkristalls beschreibt der neue Werkzeugkasten der Garchinger. Das Stichwort „Experiment“ führt uns nun auch zu dem Punkt, dass ultraflache Halbleiter, die aus einer nur ein Atom dicken Schicht bestehen, tatsächlich seit mehr als zehn Jahren herstellbar sind. Diese sogenannte Übergangsmetall-Dichalkogenide sind sozusagen das Halbleiter-Pendant zum berühmteren und zuerst entdeckten Graphen, dem ultraflachen Kohlenstoffmaterial.
Einen experimentellen Test hat dieser Werkzeugkasten bereits bestanden. Er kann Messdaten zur Absorption von Licht erklären, die an dem zweidimensionalen Halbleiter Molybdändiselenid (MoSe2) gemessen wurden. Diese Eigenschaften werden durch das Zusammenspiel der Exzitonen mit den Elektronen, also von Polaronen, gesteuert. Und dieser spezielle Effekt wurde einige Jahre zuvor zuerst in einem besonders präparierten kalten Quantengas beobachtet. Als Quantensimulator führte es so ein experimentelles Festkörperteam auf die Spur, diesen Effekt in MoSe2 zu suchen und zu finden.
Diese Geschichte aus dem produktiven Clash zweier Kulturen der Physik demonstriert so eine erfolgreiche Anwendung der Quantensimulation auf ein Festkörpersystem. Ein wichtiger Meilenstein in der Entwicklung von Quantensimulatoren ist erreicht.
(RW)