Physical Review Letters
„Finite Time Large Deviations via Matrix Product States“
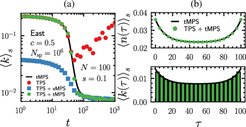
Recent work has shown the effectiveness of tensor network methods for computing large deviation functions in constrained stochastic models in the infinite time limit. Here we show that these methods can also be used to study the statistics of dynamical observables at arbitrary finite time. This is a harder problem because, in contrast to the infinite time case, where only the extremal eigenstate of a tilted Markov generator is relevant, for finite time the whole spectrum plays a role. We show that finite time dynamical partition sums can be computed efficiently and accurately in one dimension using matrix product states and describe how to use such results to generate rare event trajectories on demand. We apply our methods to the Fredrickson-Andersen and East kinetically constrained models and to the symmetric simple exclusion process, unveiling dynamical phase diagrams in terms of counting field and trajectory time. We also discuss extensions of this method to higher dimensions.
Acces to the paper: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.128.090605












