1S-2S absolute Frequency Measurement
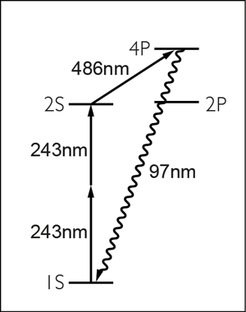
levels for the experiment
The 1S-2S transition in atomic hydrogen is a very suitable tool for precision test of fundamental physics. It fulfills the two main requirements very well:
1. With its simple structure of only one electron and one proton the theoretical treatment of hydrogen reaches a high precision on the level of 10-12 where the calculations are limited by an experimental parameter, namely the proton charge radius.
2. The meta-stable 2S state in atomic hydrogen is long-lived leading to a narrow natural line width of only 1.3Hz. Also, the transition frequency is readily accessible via two-photon spectroscopy with a continuous wave (cw) laser at 243nm.
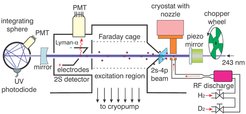
Figure 2 shows a schematic of the hydrogen spectrometer. Since there is no means to trap hydrogen in an environment suitable for precision spectroscopy we work with a cold, thermal beam of atomic hydrogen. To overcome the Doppler effect to first order, we use two photon excitation to drive the transition. In this scheme an atom is excited by a co- and a counter-propagating photon. The co-propagating photon is red-shifted by the same amount the counter-propagating photon is blue-shifted.
Molecular hydrogen is dissociated in a microwave discharge. The hot gas travels to the 6 Kelvin cold copper nozzle where the atomic hydrogen thermalizes by collisions and escapes the nozzle into the vacuum chamber. The hydrogen beam is defined by two apertures.
With the help of an enhancement cavity the power of the 243nm spectroscopy light is built up to increase the intensity and to form a standing wave necessary for two photon spectroscopy. Atoms which are excited before the excitation zone are subject to possible electric field shifts and are therefore re-pumped to the ground state by a second, blue laser. In the excitation zone the atoms are shielded against stray fields by a graphite coated Faraday cage.
Atoms which are excited to the 2S state are detected by quenching: The 2S state is so long lived that almost no spontaneous emission from the excited atoms occurs. Therefore, we force the atoms to decay by applying a small electric field. This mixes the 2S and the 2P state. The latter is short-lived and decays by emission of a Lyman-{$\alpha$} photon which we detect with a photo multiplier tube (PMT).
Chopping the excitation light and waiting for a certain delay {$\tau$} we can let the fastest atoms escape the detection region leaving only slow atoms contribution to the signal. A typical spectral line is shown in Figure 3.
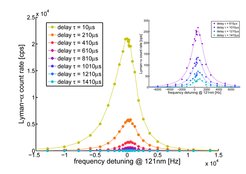
Looking at Figure 3 delay {$\tau=10\,\mu\rm{s}$} a strong asymmetry is visible. It is caused by the second order Doppler effect which is proportional to {$1/2 (v/c)^2$} which maps the Maxwellian velocity profile of the thermal atomic beam on to the spectral line. For higher delays the asymmetry vanishes at the expense of count rate. A good understanding of the velocity distribution is eminent in order to define the unperturbed frequency correctly.


