Higher-Order Symmetry-Protected Topological Phases
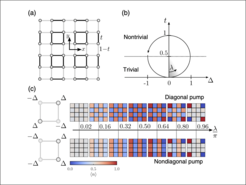
The bulk-boundary correspondence relates quantized edge states to bulk topological invariants in topological phases of matter. In one-dimensional symmetry-protected topological systems, quantized topological Thouless pumps directly reveal this principle and provide a sound mathematical foundation. Symmetry-protected higher-order topological phases of matter (HOSPTs) also feature a bulk-boundary correspondence, but its connection to quantized charge transport remains elusive. Here, we show that quantized Thouless pumps connecting C4-symmetric HOSPTs can be described by a tuple of four Chern numbers that measure quantized bulk charge transport in a direction-dependent fashion. Moreover, this tuple of Chern numbers allows to predict the sign and value of fractional corner charges in the HOSPTs. We show that the topologically nontrivial phase can be characterized by both quadrupole and dipole configurations, shedding new light on current debates about the multipole nature of the HOSPT bulk. By employing corner-periodic boundary conditions, we generalize Restas’s theory to HOSPTs. Our approach provides a simple framework for understanding topological invariants of general HOSPTs and paves the way for an in-depth description of future dynamical experiments.
Original publication:
Thouless Pumps and Bulk-Boundary Correspondence in Higher-Order Symmetry-Protected Topological Phases
Julian F. Wienand, Friederike Horn, Monika Aidelsburger, Julian Bibo, and Fabian Grusdt
Phys. Rev. Lett. 128, 246602 (2022)












