Better tests for Schrödinger cats
MPQ scientists develop new methods to test the world view of macroscopic realism
In a classical world, objects have pre-existing properties, physical influences are local and cannot travel faster than the speed of light, and it is in principle possible to measure the properties of macroscopic systems without altering them. This is referred to as local realism and macroscopic realism, and quantum mechanics is in strong contradiction with both of them. While Bell inequalities have been proven to be an optimal tool for ruling out local realism in quantum experiments, Lucas Clemente and Johannes Kofler from the Theory Division of the Max Planck Institute of Quantum Optics (MPQ) in Garching, Germany, have now shown that inequalities can never be optimal for tests of macroscopic realism. Their results reveal a hitherto unknown radical difference in the mathematical structures of spatial and temporal correlations in quantum physics, and also provide a better tool for the search of Schrödinger cat-like states (PRL.116.150401, 15 April 2016).
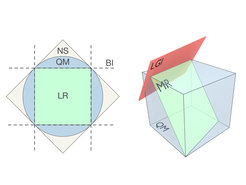
Local realism is the classical world view which assumes that objects have pre-existing properties and no influence can travel faster than the speed of light. In 1964, John Bell found that these assumptions put boundaries on the possible correlations between measurements on spatially separated objects. In local realism, spatial correlations need to obey certain inequalities, which are today called Bell inequalities.
In 1984, Arthur Fine proved that Bell inequalities are optimal in the sense that they form a tight boundary for all local realist theories. That means that the set of all Bell inequalities is both necessary and sufficient for local realism: all local realist theories obey the Bell inequalities and, in turn, obeying all Bell inequalities means that there is a local realist explanation for the observed data. Using entangled quantum states between two or more systems, such as photons or atoms, Bell inequalities can be violated. Such quantum violations were measured repeatedly over the past decades with ever increasing perfection. Thus, the world view of local realism has been conclusively ruled out experimentally.
Although quantum mechanics violates local realism, it does not allow for the transmission of information faster than light. This assumption of no-signalling is one of the pillars of special relativity theory. A violation of no-signalling would be in contradiction with causality and allow communication into the past. Quantum experiments can therefore only violate Bell inequalities, but not the no-signalling assumption.
Equally strange as the quantum violation of local realism is the famous paradox of Schrödinger’s cat, where – in a thought experiment – a cat can be put into a superposition of being both dead and alive. Until today, many physicists accept superposition states of microscopic objects but are deeply unsatisfied with the fact that quantum mechanics would in principle allow such a strange behaviour also on the macroscopic scale. The classical world view called macroscopic realism forbids such macroscopic superposition states and asserts that macroscopic objects can in principle be measured without altering their state.
In 1985, Anthony Leggett and Anupam Garg showed that macroscopic realism puts a bound on the possible temporal correlations of sequential measurements performed on a single quantum system. These temporal correlations need to obey inequalities, which are now called Leggett-Garg inequalities.
In the past years, Leggett-Garg inequalities were violated in many experiments, albeit only with microscopic quantum systems, which did not rule out macroscopic realism. Whether or not one can put macroscopic objects, such as cats, in superpositions is experimentally not yet decided and is one of the most exciting open questions in the foundations of physics.
Although local realism is about correlations in space between at least two systems, and macroscopic realism is about correlations in time of a single object, the two concepts have many analogies, and the corresponding Bell and Leggett-Garg inequalities are almost identical mathematically. However, the work of Clemente and Kofler has now revealed a remarkable and hitherto unknown disanalogy. With a sophisticated dimensional analysis of probability spaces they were able to prove that Fine’s theorem for local realism does not apply for macroscopic realism. In other words, Leggett-Garg inequalities do not form an optimal tight boundary for macrorealistic theories like Bell’s inequalities do for local realism (see Figure).
Interestingly, it is the temporal analogy to the no-signalling assumption, which does the trick. This assumption, called no-signalling in time, demands that for macroscopic objects later measurement outcomes cannot depend on earlier measurements. It holds in macroscopic realism but is violated in quantum mechanics. “In contrast to the Leggett-Garg inequalities, the combination of all no-signalling in time conditions is both necessary and sufficient for macroscopic realism. This reveals a striking difference between spatial correlations in tests of local realism and temporal correlations in tests of macroscopic realism”, Clemente explains.
Consequently, experimentalists aiming at violating macroscopic realism should stop focusing on the Leggett-Garg inequalities, which they have done for so many years now. “Leggett-Garg inequalities unnecessarily limit the parameter space in which potential violations of macroscopic realism can be found. No-signalling in time is not only a better but even optimal condition for experiments which try to test whether there can be Schrödinger cats in nature”, Kofler adds. [LC/JK]












