Quantum Information
Quantum Information is concerned with studying the way in which the laws of quantum mechanics can be used to store and process information and to perform computations. In particular, the possibility of creating superpositions of classical states, and to create correlations without a classical correspondence give rise to a wide range of new phenomena in data processing and computation.
Our research covers a wide range of topics in Quantum Information:
Quantum algorithms
Quantum computers hold the promise to outperform classical computers on certain computations by using quantum mechanical phenomena such as superpositions and entanglement.
Our research aims to understand better how quantum computers and simulators can be used for the solution of quantum mechanical problems in condensed matter physics, quantum chemistry, and high-energy physics, but also for classical optimization problems which are ubiquitous in industrial applications.

Besides algorithms for future fault-tolerant quantum computers, we explore ways in which intermediate-scale near-term quantum devices might offer an advantage over classical computers already today. Our investigations also encompass the development of algorithms specifically designed for digital or analogue quantum computers, and the evaluation of the capabilities and limitations of intermediate-scale near-term quantum devices in comparison to classical computers. Through collaborative efforts, also with experimental groups, our aim is to advance the field of quantum algorithms and contribute to realizing practical quantum computing.
Quantum information aspects of tensor networks
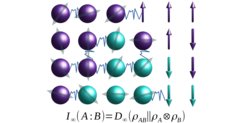
Entanglement – correlations between particles which cannot be explained classically – is arguably the most peculiar feature of quantum physics. Tensor Networks (TN) provide a physically relevant class of many-body states and operations with controllable entanglement complexity. Utilizing tools from Quantum Information theory, we work on the classification of TN states and operations, based on their structure, gauge freedom and symmetries. We devise protocols for their implementation on near term quantum devices, for which restrictions arising from the local interactions and noise constitute important limitations. We develop rigorous methods to approximate the ground states of Hamiltonians with states of low entanglement, theoretical energy bounds that can be used to certify the results of numerical simulations with tensor networks, and study typical properties of different TN families.
Certification and characterization of quantum devices
We develop techniques for characterizing and benchmarking quantum devices, as well as fundamental tests of quantum mechanics to distinguish it from classical theories.
Among other tasks, we study the verification of quantum computers, which entails certifying that the output of a quantum device is the desired one using limited classical resources. This is a challenging task, but essential for building trust in quantum devices.
Additionally, we study the limitations of both digital and analog quantum devices in the presence of errors. We aim to characterize how noise spreads and affects quantum computations, and to discern whether there is a trade-off between the quantum properties that may offer a computational advantage and noise disturbance.
Classical and quantum machine learning
Machine learning has revolutionized various scientific and engineering communities in the past few decades. Quantum theory, on the other hand, is arguably the most successful quantitative theory of nature. At the Theory division, we are exploring the rapidly growing field of quantum machine learning, which fuses together machine learning and quantum theories to bring new possibilities to both fields. We study how classical machine learning techniques can be applied to accelerate scientific discovery in quantum science. At the same time, we explore the use of quantum information language to diagnose and enhance the efficiency of classical machine learning algorithms.
Moreover, quantum computers have the potential to solve many problems significantly faster than classical computers. We investigate how quantum computers can enhance the representations and speed up the inferences of machine learning models, unlocking new possibilities in application areas such as natural language processing and computer vision.


