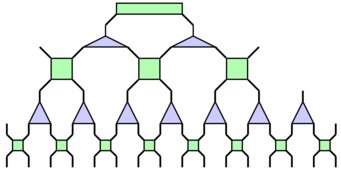
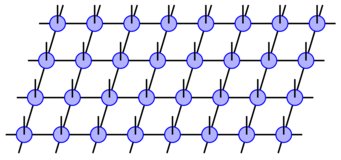
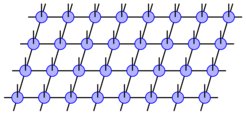
Quantum Many-Body Physics
Systems composed of multiple quantum components exhibit rich physical phenomena and can give rise to the most interesting macroscopic properties (e.g. high-temperature superconductivity or thermalization). Most such systems are very hard to solve, and it is of fundamental interest to develop techniques that allow us a better understanding of these phenomena.
The theory division investigates these problems from different perspectives:
Tensor networks - theory and numerics

Describing in full generality the space of quantum states for a many-body system is a challenging task due to the mathematical structure of Hilbert spaces. To circumvent this problem, Tensor Networks States (TNS) are proposed as a more manageable discrete ansatz to be used both numerically and analytically to tackle otherwise impossible problems, either as a variational solution or an exact one. In the analytical study of TNS, we ask questions such as: How broad is the class of TNS? Are TNS enough to classify all phases of matter?
How efficiently can we represent a target state or Hamiltonian with TNS? What are the limits of TNS and how can we extend the ansatz to include previously unreachable states? To answer these questions we borrow tools from both quantum information theory as well as quantum many-body theory, such as condensed matter physics or quantum field theory.
As an example, it is known that TNS can classify most topological orders and we are working towards a complete classification by extending the ansatz to the continuum to include chiral topological order. Other examples include extending the scope of current canonical forms of TNS to encompass a broader range of quantum states.
In the numerical aspect, tensor network methods have revealed themselves as the most powerful tools in studying strongly correlated quantum many-body systems. They provide ansatzes to efficiently describe states fulfilling the area law of entanglement and are successfully applied in a variety of problems including approximating ground and low-lying excitation states, thermal states as well as short time evolutions. We investigate the numerical application of Tensor Network techniques to different quantum many-body problems, especially in research areas where the applicability of TNS has not been fully exploited. We also investigate the limitations of the existing techniques and their possible extensions to tackle open problems in novel ways.
Solvable models and quantum dynamics

Solvable models give us a way of understanding otherwise inaccessible quantum dynamics. They provide crucial insights into the behavior of correlation functions, entanglement evolution, and other quantities. Two classes of examples, that we study, are characterized by a property that their evolution is either unitary or unital in the space direction. Surprisingly, these classes contain chaotic, integrable, and free models, showing different physical behaviors.

Solvable models can also give precise insights into otherwise complicated phenomena in correlated systems. As an example, we investigate doped quantum magnets and the binding of such dopants in these systems, which is believed to yield very valuable insights into the mechanisms of high-temperature superconductivity. Studying this in so-called Bethe lattice geometries allows us to describe the non-equilibrium dynamics of single dopants exactly, and in great detail how these dopants interact via the underlying spin-lattice.
Gaussian states and beyond
Performing computations for systems involving many quantum particles, be it bosons of fermions, poses a formidable challenge as the complexity of the corresponding quantum states grows. In the limit in which interactions become weak, however, Gaussian states can be used as a highly efficient ansatz, greatly increasing our understanding and computational capabilities. In our group, we use Gaussian states as a tool to gain understanding about e.g. the performance of near-term quantum simulators. We also investigate the applicability regimes of Gaussian tensor networks, an ansatz that combines the advantages and limitations of Gaussian states and tensor networks. Additionally, we study and propose extensions into the non-Gaussian realms to better represent systems where interactions play a significant role while trying to keep computational performance.
Lattice gauge theory
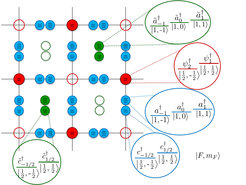
Lattice gauge theories (LGTs) are perhaps the most successful numerical approach at simulating high energy physics models. However, the classical methods to LGTs suffer from the sign problem in the Monte Carlo simulations that limit their scope. We investigate novel, quantum information inspired approaches to develop new techniques for probing these models. One avenue of research involves applying tensor network (TN) methods to LGTs. The TNs have proved themselves at efficiently characterising strongly-correlated many body systems. Furthermore, the approach does not suffer from the sign problem, allowing to probe real time evolution, which is hard with conventional LGT methods. We develop new ways to characterise LGTs using tensor network ansatzes and investigate new methods that could compliment the standard Monte-Carlo approaches.
Additionally, we research the possibilities of LGT simulations on quantum computers and quantum simulators. The advance of quantum technologies could provide a new way of investigating LGTs by Hamiltonian simulation avoiding the sign problem. We research how to map the LGT models to quantum devices, the quantum algorithms and the resources required to simulate them, and the associated challenges.
Quantum many-body physics group members