Playing Pool with Excitons
New toolbox for the simulation of ultra-flat semiconductors developed
Semiconductors play an important role, be it in electronics, optoelectronics or photovoltaics. But like other solid bodies, they are quantum many-body systems. Therefore, a calculation of their material properties would overburden conventional computers. Instead, this task could be performed by a quantum system with comparable properties that is fully controllable from the outside. This dream of a quantum simulator has been around for a long time. Now the junior theory research group led by Richard Schmidt at the Max Planck Institute for Quantum Optics in collaboration with colleagues at the University of Hamburg and ETH Zurich has successfully completed a work that can explain a successful quantum simulation of certain properties of an ultra-flat semiconductor. More than that, they have developed a new toolbox to theoretically describe these two-dimensional semiconductors.
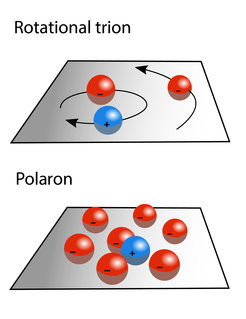
Upper graphic: On the left is the exciton, which consists of a hole (blue, positively charged) and an electron (red, negatively charged). It has just "captured" another electron (right) and thus forms a trion, a quasi-particle consisting of three particles.
Lower graphic: In the two-dimensional semiconductor, freely moving electrons gather around an exciton (center) and together they form a larger quasiparticle, the polaron.
Not only in human society in general, but also in physics there are different “cultures”. The latest paper from the junior theory research group led by Richard Schmidt at the Max Planck Institute of Quantum Optics draws a connecting line between two of such cultures: Quantum Optics and Solid State Physics. And it is part of a research direction that is developing a kind of analog quantum computer, so-called quantum simulators. The idea goes back to the famous American theorist Richard Feynman.
The work of the theorists in Garching has now been published as an Editor's suggestion in the journal "Physical Review B". It is about a solid-state system with special properties that were first observed in ultracold quantum gases just a few years earlier. Such gases are a popular object of investigation in quantum optics and, as a quantum simulator, have made it possible to predict novel properties of solid-state systems that have recently been found in experiments.
To understand the background, it is helpful to first appreciate the idea of quantum simulation in this context. Solids consist of an extremely large number of particles. In solids, the atoms with their electrons are "stacked" in a very small space to build a crystal lattice and they thus form a complex quantum many-particle system. Such systems are the speciality of Richard Schmidt, the head of the research group. This many-body system can collectively produce complex properties which build the basis for the electronics and optoelectronics in semiconductor materials ranging from LEDs to photovoltaics.
The fundamental problem of theoretical physics is that although it can formulate the exact quantum mechanical equations for such a many-body system like a solid, it cannot solve them exactly. Therefore, theorists work with highly simplified solutions. In principle, more precise results could be obtained by simulation, i.e. a virtual replica of the solid under consideration on the computer. However, this fails because of the complex interactions between the quantum particles. Even a quantum system consisting of very few particles would cause the required computing power to explode to such an extent that even today's best supercomputers would be overwhelmed.
Feynman's smart idea of a quantum simulator
Back in the 1980s this dilemma gave Richard Feynman a brilliant idea: could it be possible to simulate such a quantum many-body system using a quantum system of similar power? This other quantum system should have comparable properties, but be easily accessible and thus fully controllable – in contrast to typical solid state systems.
This is where the ultracold quantum gases of quantum optics, such as studied at the Max-Planck Institute in Garching, come into play. In principle, they provide exactly what characterizes a quantum simulator: they are fully controllable from the outside and can thus be programmed with the properties of a solid state system. To produce an ultracold quantum gas, a cloud of atoms floating in a vacuum is cooled to extremely low temperatures, only a few millionths of a degree above absolute zero. At such low temperatures it is possible to capture atoms in the intersections of a spatial grid of laser beams. If these atoms have suitable properties, they can simulate the behaviour of electrons in a solid state crystal. Here it is essential to realize that electrons determine the essential properties of a solid, such as its hardness, whether it can convert light into electric current or vice versa – or its electrical conductivity, and even superconductivity in certain materials.
That's the idea. In practice, however, the challenge for quantum optics for many years has been to correctly reproduce the interaction between the electrons in a solid. Electrons as elementary electric charges still interact with each other over relatively large distances, via electric and magnetic fields. So they influence not only their nearest neighbours, but also the neighbours after that and so on. In contrast, cold atoms in a quantum gas behave more like billiard balls: They interact by impact essentially only with their nearest neighbors.
The exciton as a billiard ball
So in order to be able to apply such a quantum simulator to a solid state, it would be helpful to identify particles in the solid state system that interacted more like billiard balls. Fortunately, these exist in the form of so-called excitons. These particles are found in every normal semiconductor, for example in LED based displays or vice versa in a photovoltaic system producing electricity.
An exciton can form when a quantum of light, a photon, strikes an electron in a semiconductor material. If the energy of the photon is just right, the electron absorbs this energy, detaches from its atom and can move freely through the semiconductor. This is the basic process that underlies the conversion of light into electricity. On the original place of the electron a hole is now however left behind, which again can effectively move through the crystal lattice as an electrically positive charge. The electron and the hole attract each other electrically and together they form a so-called quasi-particle, the exciton, which can now also move freely through the semiconductor.
“You can think of the exciton roughly like a hydrogen atom," explains Richard Schmidt: "The hole corresponds to the proton in its atomic nucleus.” And this exciton behaves more like a billiard ball, which can only hit another ball in direct contact – like the atoms in cold quantum gas. However, the electron and the hole that form the exciton in ordinary semiconductors are quite far apart. “That could be ten or more nanometers," says Christian Fey, postdoc in the Garching group and first author of the article. If there are other freely moving electrons in a normal, three-dimensional semiconductor, they not only surround the exciton, they also penetrate and decompose it very quickly. This happens already at electron densities that are technically relevant.
Ultra-flat semiconductors as ideal simulation object
A two-dimensional semiconductor, on the other hand, is so flat that there are no electrons above and below the exciton that can weaken it. Thus the exciton can even survive if there are additional electrons in the plane. And not only that: it can also influence the electrons around them so that a so-called polaron is created. This is a many-particle object in which the exciton is dressed in a cloud of electrons. The mass of the exciton is effectively increased because it has to pull this cloud with it through the solid. As an alternative to polaron formation, the exciton can also form a larger quasi-particle, a "trion", with another electron as a third particle. "It's like a solar system with a star and a planet that captures a comet passing by from the cosmos as a third body," explains Schmidt. “We have even theoretically found a new state in which the electron orbits in opposite direction around the exciton," Fey adds, "that would be like the comet running around the star in the opposite direction to the planet.”
While this state has not yet been found experimentally, it is along the physical properties of a two-dimensional semiconductor crystal that is described in the Garchingers' new toolbox. The keyword "experiment" now also leads us to the point that ultrathin semiconductors that consist of a layer only one atom thick, have been produced for more than ten years. These so-called transition metal dichalcogenides are the semiconductor cousin of the more famous graphene, the ultrathin carbon material.
Applied to these materials, the toolbox developed in Garching has already passed an experimental test. It can explain the measured data on the absorption of light observed in the two-dimensional semiconductor molybdenum diselenide (MoSe2). These properties are controlled by the interaction of excitons with electrons, i.e. polarons. Remarkably, this special effect was observed first a few years earlier in a specially prepared cold quantum gas. As a quantum simulator, it led an experimental solid-state team to search for and find this effect in MoSe2.
This story of a productive clash of two cultures of physics thus demonstrates a successful application of quantum simulation to a solid state system. An important milestone in the development of quantum simulators has been reached.
(RW/KJ)












