Rydberg Quantum Photonics
We experimentally investigate ultracold atomic gases. In recent years our focus has been on studies of large optical nonlinearities at the single-photon level created by coupling photons to atomic Rydberg excitations.
Single photon transistor
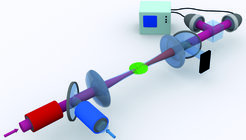
Toggling an all-optical switch with a single photon is a nontrivial task because the nonlinearities of conventional nonlinear crystals are tiny at the single-photon level. We use a combination of electromagnetically induced transparency and Rydberg blockade in an ultracold atomic gas to overcome this limitation. In this way, we managed to realize a single-photon transistor. In this device, an incoming control light pulse containing only one photon enters an ultracold atomic gas. This control pulse changes the transmission of a subsequent target light pulse through the gas. We observed a gain of 20, i.e. a single control photon causes the number of transmitted target photons to change by 20. As a first application, we experimentally demonstrated the nondestructive optical detection of a single Rydberg excitation in the atomic gas with a fidelity of 86%.
Photon-photon quantum gate
A variety of proposals suggests that the giant optical nonlinearity attainable with Rydberg atoms should allow one to build a quantum gate between two optical photons. Based on a variation of the single-photon transistor scheme, now with detuned laser light, we demonstrated the first photon-photon quantum gate based on Rydberg interactions. Unfortunately, the success probability of this gate was only 3% on average. The dominant limitation of this experiment was loss of atomic coherence caused by atom-atom collisions. To mitigate this problem, we built a new vacuum system, which houses an optical resonator with a moderate finesse of a few hundred. Placing the atomic ensemble inside this resonator allows it to operate the experiment at much lower atomic density, which results in much longer coherence times. With this strategy, we recently managed to push the success probability of the photon-photon quantum gate to 42%, clearly outperforming the previous record of 11%, set 20 years ago in an experiment based on linear optical quantum computing. Our next goal is to study Schrödinger cat states of optical photons produced with this quantum gate.
Third Party Funding
We acknowledge financial support from Deutsche Forschungsgemeinschaft via the priority program 1929 GiRyd and via the cluster of excellence MCQST.
Open Positions
If you are interested in joining the group, please consult the Open Positions page, and contact Dr. Stephan Dürr or Prof. Gerhard Rempe.
