The Hydrogen 1S-3S Transition
Similarly, to the 2S-4P experiment, the purpose of measuring the 1S-3S transition freuquency in atomic hydrogen is to test the theory of Quantum Electrodynamics (QED). Intuitively, one would say that such a test is conducted by comparing theoretical predictions with experimental observations. Unfortunately, it is not that simple. The theoretical expressions involve parameters that cannot be computed from first principles and hence need to be determined experimentally. With n such parameters one needs n measurements to get a hold of their values. Clearly, this does not test the theory since the parameters can always be chosen to match theory and experiment. To test a theory with parameters one needs to measure more independent quantities (here transition frequencies) than there are parameters. When it comes to testing QED with hydrogen spectroscopy, we are left with 2 free parameters: the Rydberg constant Ry and the charge radius of the proton rp. Further parameters, like the fine structure constant and the electron to proton mass ratio can be determined more precisely from other experiments, that are more sensitive to those. In the spectrum of atomic hydrogen, the 1S-2S transition frequency is measured most accurately by far, due to its very small natural linewidth. Therefore, other measurements can be compared to each other, by calculating the values of Ry and rp, they yield together with the 1S-2S measurement.
Apart from hydrogen spectroscopy, the charge radius of the proton can also be measured by electron scattering experiments or calculated, using quantum chromodynamics. Unfortunately, those methods do not yet reach the required accuracy. The contribution of the size of the proton to our measurements is truly tiny. However, since QED calculations of the hydrogen spectrum are among the most accurate calculations physics has to offer, even a tiny contribution is important. In muonic hydrogen, where the electron is replaced by its heavier brother the muon, this contribution much larger. Therefore muonic hydrogen spectroscopy yields a much more accurate value for rp, even though the measurement accuracy is much less. The figure summarizes the situation as of 2020.
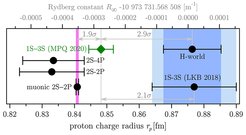
The proton charge radius measurements (bottom axis), as obtained from various experiments, partially disagree, preventing a verification of QED on the level of experimental uncertainties. Combining the 1S-2S and the 1S-3S (MPQ 2020) transition frequencies gives a significantly smaller value than the previous world data (H-world) obtained by using all hydrogen measurements (15 lines) available for the most recent published CODATA adjustment. In contrast, a continuous wave measurement of the 1S-3S transition frequency performed by our colleagues at the Laboratoire Kastler Brossel (LKB 2018) confirms the CODATA value. Our result is in reasonable agreement with our value derived from the 2S-4P measurement, with a radio frequency measurement of the 2S-2P transition, and with the value obtained from muonic hydrogen. Here we are not interested in the actual values of the parameters but in the consitency of the various values. The consitency check is the QED test.
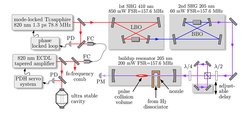
Two-photon direct frequency comb spectroscopy
Similar to the 1S-2S experiment, we use a cryogenic atomic beam and Doppler free two-photon spectroscopy with counter-propagating laser beams. This laser is frequency doubled twice (SHG) to reach the transition wavelength of 205nm. In contrast to the 1S-2S experiment we use a pulsed mode locked laser rather than a continuous wave laser. With an adjustable delay line we generate counter propagating pulse trains that meet at a small pulse collision volume in the center of the 205nm buildup resonator. Doppler free excitation takes place only within this volume. Pulsed excitation has several advantages adapted to the 1MHz linewidth without limiting the observational linewidth due to time of flight broadening. It allows efficient collection of the signal and limiting background light. More importantly, a small volume can be easily and homogenously shielded against stray electric and magnetic fields. By varying the distance to the hydrogen nozzle collisional shifts can be well characterized. Finally, the Doppler sensitive signal collected outside excitation volume, that is very much independent of laser frequency, serves as a normalization signal to cancel fluctuations of atomic flux and laser power. This feature significantly reduces the noise.
In the frequency domain the pulse trains are described by a regular spaced frequency comb. Pairwise addition of all comb modes provides an efficient excitation of the 1S-3S transition. It is important to note that the laser linewidth that enters the line shape of the Doppler free signal, is given by the width of the individual modes of the frequency comb rather than the inverse pulse duration. At the same time the frequency doubling process is very efficient due to the increased peak power in a pulsed laser.
High Precision Spectroscopy - 360° VR Labtour at the MPQ (with Derya Taray)
Current Members
Alexey Grinin, Derya Taray, Thomas Udem
Former Members
Arthur Matveev, Dylan Yost, Elisabeth Peters, Sascha Reinhardt
If you are considering joining our team as a Bachelor, Master or PhD student, or as a Postdoc, please email to: Thomas Udem


