With single laser pulses on single molecules
Physicists at MPQ succeed in resolving the internal dynamics of individual molecules using UV femtosecond laser pulses
Nowadays, large laser systems provide ultra-short light pulses of very high intensity which – in principle – allow the imaging of matter and its dynamics on atomic scales, down to a single molecule or a virus. However, current methods fall short in efficiency to overlap a target molecule in a deterministic way. Physicists around Prof. Tobias Schätz (Max Planck Institute of Quantum Optics and Universität Freiburg) have now found a possible way out. Using the well proven concept of ion traps they store a single molecule at a precisely known position and then hit it in a deterministic way with single laser pulses that are provided by the Laboratory for Attosecond Physics at MPQ (Nature Physics, AOP, 5 February 2012, DOI 10.1038/NPHYS2214). Though still restricted to pulses in the UV range this method makes it possible to resolve the internal dynamics of a single molecular ion consisting of a magnesium ion and a hydrogen atom. “However, this scheme could become a standard technique for investigating large biomolecules, if X-ray laser pulses can be applied”, Tobias Schätz points out.
At present there is no satisfying method for investigating the structure of large and complex molecules, e.g., proteins. The standard technique is based on the diffraction of X-rays in crystals and fails in this case, because many biological molecules are difficult or impossible to crystallize. Diffraction experiments on single molecules with low-intensity sources require long exposure times in order to reach the number of about 1013 photons which is necessary to achieve an image. This leads to radiation damage of the target particle and, furthermore, excludes the temporal resolution required to analyze short-lived intermediate products or fast structural changes.
A new generation of X-ray femtosecond lasers promises to overcome these limitations. Light pulses comprising a huge number of photons within a period of a few femtoseconds produce images of a single molecule before the radiation damage becomes visible (1 femtosecond corresponds to 10-15 seconds). In addition, the beam diametre of the laser has to be focused down to the size of a molecule, about a tenth of a micrometre. This has been accomplished already. The challenge is now to prepare a single molecule so reliable that it can be deterministically placed within the laser pulse.
In the past couple of decades ion traps have provided unique control capabilities for charged particles. An ion trap is basically a small vacuum chamber containing four electrodes which are switched rapidly between minus and plus, at frequencies in the radio frequency range (107 Hertz). Under the influence of these quickly changing electrical fields a single ion (i.e. an electrically charged atom), which has been cooled down to very low temperatures, gets trapped in the centre of the chamber. Isolated from the environment the 'floating' ion can remain there for hours. If several ions are guided into the trap a structured pattern evolves, due to their mutual repulsion. This reminds of a solid state crystal, yet, the lattice sites are much easier to resolve, since the distances between the ions are a 100 000 times larger.
In contrast to atomic ions molecules are much more difficult to trap because they cannot directly be cooled. The MPQ team has now resumed to a trick: they embed the molecule into a crystal formed by cooled atomic ions. The experimental set up consists of two ion traps connected in series. In the first trap the molecular ion is prepared in a photochemical reaction from magnesium and hydrogen, i.e., each molecule consists of a positively charged magnesium ion and a hydrogen atom. These molecular ions are transferred into a second ion trap already filled with atomic magnesium ions which have arranged themselves into a regular pattern, keeping a distance of 10 micrometres from each other. In this very cold environment also the single molecule comes to a rest and replaces one of the atoms in the ion crystal. Whereas the atomic ions emit light by fluorescence, the lattice site occupied with the molecule remains dark. The absolute position of the molecular ion can then be deduced by detecting the fluorescence light of its neighbours with an accuracy of less than a micrometre.
Now the conditions are set for hitting the single molecule with a femtosecond laser pulse at a probability of almost 100 percent. In the beginning the molecule finds itself in a vibrational ground state. With a first so-called pump pulse it gets excited into a state in which its two components – the magnesium ion and the hydrogen atom – oscillate with a period of 30 femtoseconds. A short time later a second pulse ‘probes’ in which phase of the oscillation cycle the molecule is at that very moment. At the turning point of the oscillation, after 15 femtoseconds, the distance between the particles has reached its maximum. If the probe pulse hits the molecule at that time, the dissociation probability is particularly high. The breaking of the chemical bond is signaled by the disappearance of a non fluorescing dark spot.
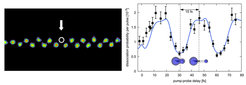
“In our experiment we should be able to provide the molecules at the rate of the laser pulses, i.e., about a hundred per second”, Tobias Schätz explains. “So each time a molecule is damaged by radiation it can be replaced by an identical one. As we vary the delay between pump- and probe-pulse we can resolve the vibrational dynamics of the bi-atomic molecule. This is due to the fact that the laser pulse duration of a few femtoseconds is much shorter than the molecular oscillation cycle.”
The experiment described here is a demonstration of the feasibility and the potential of the new technique which for the first time combines ion traps with classical pump-probe set-ups. The use of X-rays instead of UV-pulses will make it possible to apply the technique to biomolecules which in nature often show up as charged articles. The high intensity and the short duration of the X-Ray pulses will allow obtaining useful information on the structure of the molecule before it suffers from radiation damage. In the future experiments of that kind could be the key to investigate single complex molecules with the necessary precision and efficiency. Olivia Meyer-Streng
Contact:
Prof. Dr. Tobias Schätz
Max Planck Institute of Quantum Optics
Hans-Kopfermann-Straße 1, 85748 Garching
Phone: +49 (0)89 32 905 -199 / Fax: -311
E-mail: tobias.schaetz@mpq.mpg.de
Dr. Olivia Meyer-Streng
Press & Public Relations
Max Planck Institute of Quantum Optics
Phone: +49 (0)89 / 32 905 -213
E-mail: olivia.meyer-streng@mpq.mpg.de
