Physical Review Letters
"Topological Lower Bound on Quantum Chaos by Entanglement Growth"
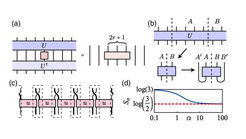
A fundamental result in modern quantum chaos theory is the Maldacena-Shenker-Stanford upper bound on the growth of out-of-time-order correlators, whose infinite-temperature limit is related to the operator-space entanglement entropy of the evolution operator. Here we show that, for one-dimensional quantum cellular automata (QCA), there exists a lower bound on quantum chaos quantified by such entanglement entropy. This lower bound is equal to twice the index of the QCA, which is a topological invariant that measures the chirality of information flow, and holds for all the Rényi entropies, with its strongest Rényi-∞ version being tight. The rigorous bound rules out the possibility of any sublinear entanglement growth behavior, showing in particular that many-body localization is forbidden for unitary evolutions displaying nonzero index. Since the Rényi entropy is measurable, our findings have direct experimental relevance. Our result is robust against exponential tails which naturally appear in quantum dynamics generated by local Hamiltonians.
Access to the paper: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.126.160601












