Magic numbers of quantum matter revealed by cold atoms
Scientists extract the topological number of an artificial solid subjected to extreme effective magnetic fields
Matter forms remarkable phases when it is immersed in extreme environments, such as strong magnetic fields and low temperature. Under these conditions, materials can reach unusual regimes where their electrical properties present universal and exotic behaviours, e.g. dissipationless currents and quantized electrical resistance. This physical framework sets the stage for new phases of matter, the topological states, which are described by magic (topological) integers. They are mathematical numbers used to classify geometric objects [e.g. the number of holes in a surface, Fig. 1a], and which remain immune to deformations. The outstanding fact that quantum states of matter can be associated with topological numbers guarantees the robustness of their unique electrical properties against perturbations. This suggests numerous promising technological applications, e.g. in spintronics and quantum computation, hence motivating the search for novel topological states of matter in laboratories.

Fig. 1: The classification of geometric objects and quantum matter. a. Topology classifies these three objects in terms of the number of handles g. The doughnut is equivalent to a mug (g=1), but differs from a ball (g=0). b. Illustration of an atomic gas trapped in a two-dimensional optical lattice: (left panel) a conventional lattice, and (right panel) a lattice subjected to an effective magnetic field. The related quantum phases are associated with different topological (Chern) numbers, schematically illustrated by the ball and the doughnut, respectively.
Topological states were discovered in the context of the quantum Hall effect, i.e. through studies of the electrical resistance in materials subjected to strong magnetic fields. After reaching sufficiently low temperatures, the measured resistance was found to form robust plateaus when varying the magnetic field, a behaviour which was shown to be independent of the sample. Surprisingly, this universal physical property - the quantum Hall effect celebrated by the Nobel prize in 1985 - appeared to be rooted in topology: each resistance plateau is dictated by a topological number, the Chern number. "The beauty of this result relies in the fact that these magic mathematical numbers appear as intrinsic properties of the electrons moving in the material; it is intriguing that these abstract numbers actually lead to extraordinary observable phenomena", says theorist Nathan Goldman.
An interesting route for the search of topological phases of matter is offered by synthetic materials, which consist of ultracold atomic gases controlled by light. In these highly versatile experiments, neutral atoms are trapped in a periodic landscape created by standing waves of lasers. Cold atoms moving in these optical lattices have proven to be very well suited to mimic the dynamics of electrons propagating in real materials. However, in contrast to electrons, cold atoms are charge neutral; hence, they do not exhibit the Hall effect in the presence of a magnetic field. To overcome this limitation, new experimental techniques were developed in Munich in order to engineer effective magnetic fields for neutral atoms. In such arrangements, cold atoms behave as charged particles subjected to strong magnetic fields, offering a new platform to study the Hall effect and topological phases in a highly controllable and clean environment.
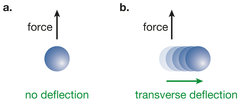
Fig. 2: The Chern-number measurement using an external force. a. The atoms are not deflected in a conventional lattice with zero Chern number. b. When the Chern number is νch = 1, the atoms are deflected transverse to the force.
The optical-lattice setup realized in the Munich experiment has been specifically tailored so as to exhibit topological properties (Fig. 1b). Indeed, when inducing an effective magnetic field in the lattice, the atomic gas is characterized by a non-zero topological Chern number νch = 1. Nathan Goldman explains: "In this configuration, and in direct analogy with the electric Hall effect, the atomic cloud is expected to experience a characteristic transverse motion in response to an applied force (Fig. 2). Moreover, our theory predicts that this transverse drift should be directly proportional to the topological Chern number (νch = 1)". The experimentalists applied a force to their optical-lattice setup and analyzed such a displacement by taking snap-shots of the cloud. From this sequence of images, they determined an experimental value for the Chern number νexp = 0.99(5) in excellent agreement with theory. This result constitutes the first Chern-number measurement in a non-electronic system. In contrast to electronic measurements, which are based on currents flowing along the edges of the sample, the Munich Chern-number measurement directly probes the topological nature of the bulk.
These measurements constitute an important step towards the realization and detection of topological states with ultracold atoms. Including interactions between the atoms could generate novel and exciting phases, such as the much sought after fractional Chern insulators. [N.G. and M.A.]













