PRX Quantum
"Algorithms for Quantum Simulation at Finite Energies"
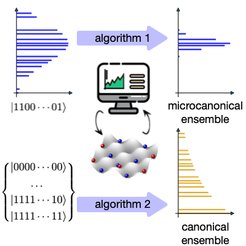
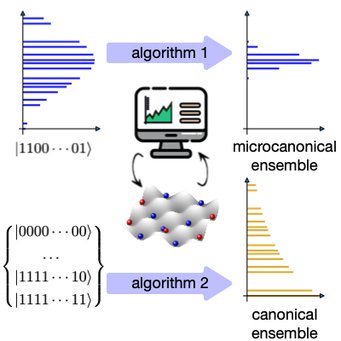
We introduce two kinds of quantum algorithm to explore microcanonical and canonical properties of many-body systems. The first is a hybrid quantum algorithm that, given an efficiently preparable state, computes expectation values in a finite energy interval around its mean energy. This algorithm is based on a filtering operator, similar to quantum phase estimation, which filters out energies outside the desired energy interval. However, instead of performing this operation on a physical state, it recovers the physical values by performing interferometric measurements without the need to prepare the filtered state. We show that the computational time scales polynomially with the number of qubits, the inverse of the prescribed variance, and the inverse error. In practice, the algorithm does not require the evolution for long times, but instead a significant number of measurements in order to obtain sensible results. Our second algorithm is a quantum assisted Monte Carlo sampling method to compute other quantities that approach the expectation values for the microcanonical and canonical ensembles. Using classical Monte Carlo techniques and the quantum computer as a resource, this method circumvents the sign problem that plagues classical quantum Monte Carlo simulations, as long as one can prepare states with suitable energies. All algorithms can be used with small quantum computers and analog quantum simulators, as long as they can perform the interferometric measurements. We also show that this last task can be greatly simplified at the expense of performing more measurements.
Access to the paper: https://journals.aps.org/prxquantum/abstract/10.1103/PRXQuantum.2.020321